Data Structures

Bitwise Operations

Operators

Shift Left <<
Shift Right >>
Or |
And &
Invert ~
Exclusive Or ^

Common Operations

In each of the following cases, it should be noted that each byte in hex format is two digits (0x00). Therefore, moving a hex value by one byte is equivalent to shifting it 8 bits, or 0x00FF << 8 = 0xFF00, and moving the hex value one space is half a byte, or 4 bits (a nibble).

Set Bit

To set the th bit in value , shift (0x000000001) by n bits and AND them. x & (1 << n)

Clear Bit

To clear the th bit in value , shift (0x000000001) by n bits and invert the ANDed value. x & ~(1 << n)

Flip Bit

To flip the th bit in value , shift (0x000000001) by n bits and XOR them. x ^ (1 << n)

Clear

To clear all values, AND the value with 0xFFFF. x & 0xFFFF

Little Endian to Big Endian

A little-endian system, in contrast, stores the least-significant byte at the smallest address.

Binary (Decimal: 149)	`1`	`0`	`0`	`1`	`0`	`1`	`0`	`1`
Bit weight
Bit position	MSB							LSB

In the case of the value 0x12345678, the least significant byte of this value 0x78 is stored in the lowest little Endian address, and subsequent bytes are stored in the next locations. The least significant byte can be considered the byte with the lowest value, when evaluated in typical bitwise fashion: 0x78563412

0x78 (0x004000)
0x56 (0x004001)
0x34 (0x004002)
0x12 (0x004003)

Big Endian to Little Endian

In a Big Endian representation of 0x12345678, the most significant byte (0x12) is stored at the lowest memory address: 0x12345678

0x12 (0x004000)
0x34 (0x004001)
0x56 (0x004002)
0x78 (0x004003)

To reverse these positions, the bytes can be isolated and bit-shifted by the appropriate number of bits to form the appropriate order.

(0x12345678 & 0x000000FF) << 24
(0x12345678 & 0x0000FF00) << 16
(0x12345678 & 0x00FF0000) << 8
(0x12345678 & 0xFF000000) >> 24

Array

Arrays are collections of same-type data items stored in a contiguous memory location. Knowing the data type, each element is located at an offset based on that data size. In other words, for int data[] the data at data[1] is located at data[0] + sizeof(int).

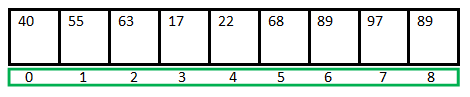
array

Arrays in C

There is no index out-of-bound checking in C, so if access goes beyond the index boundaries of the array (0-(n-1)) there will be undefined behavior.

Static vs. Dynamic Arrays

Pointer and array accesses can be treated the same way in C, either by accessing the values by using the [] operator, or by incrementing the value of the pointer.

Static Arrays

In C, the size of an array should be decided at compile time by defining the array size either by declaring an array with size constraints such as arr[10] or by using malloc to define the required size. At run time this size will be used to allocate the required memory space.

Dynamic Arrays

In C++ an array can be passed a variable and the size can be determined for the memory allocation at run time.

C Strings

A C string is a pointer to an array of char data items which is terminated by the NULL character at the size limit. So, a char array of n items will contain data at elements 0-(n-1), while the value at n will be NULL. This allows for string operations to check for the boundary of memory space for the string object.

Matrix

matrix

Normal Declaration

Dynamic Declaration

Linked List

Unlike arrays, Linked Lists are dynamic and can grow by pointing to non-contiguous locations in memory using pointers. Extra memory is required when representing each pointer in the linked list, but it allows for easily inserting and deleting objects in the linked list.

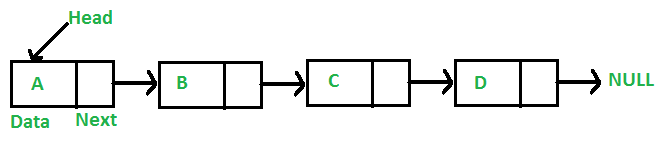
linkedlist

Each node in the linked list consists of its data, and a pointer to the next object in the linked list. In the case that the head of the linked list is null.

Inserting

Deleting

Circular Linked List

Inserting

Deleting

circularlinkedlist

Doubly Linked List

doublylinkedlist

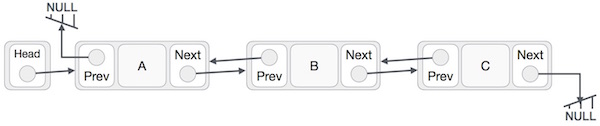
Inserting

Deleting

Binary Tree

binarytree

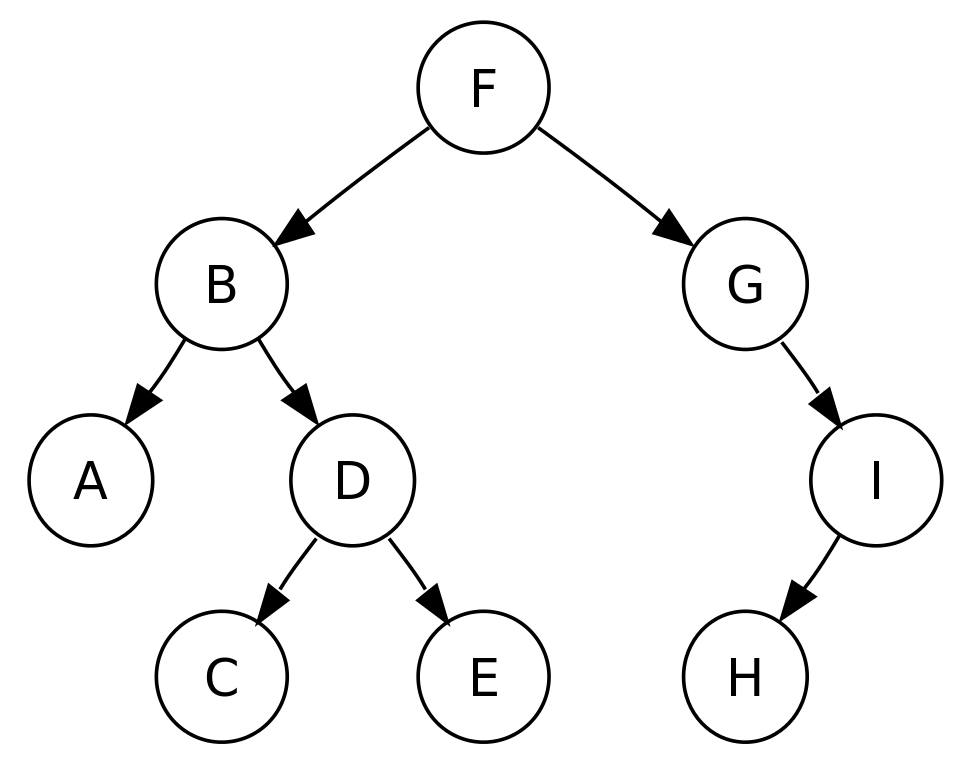
A Binary Tree is any tree organized in which each node, or root has at most two children, or leaves, hence binary, designated left and right.

Depth First Traversal

Depth First Traversal traverses the tree to its extents before backtracking and completing the traversal. It will explore until it reaches nodes with no children before moving to the nearest neighbor. The order of traversal can be categorized into Pre-Order, In-Order and Post-Order which determine which order the nodes (Left, right,center) are visited.

Pre-Order Traversal

void pre_order(struct Node* n) {
    // print n->value

    if (n->left)
        pre_order(n->left);

    if (n->right)
        pre_order(n->right);
}

void pre_order(struct Node* n) {
    // print n->value

    if (n->left)
        pre_order(n->left);

    if (n->right)
        pre_order(n->right);
}

In-Order Traversal

void in_order(struct Node* n) {
    if (n->left)
        pre_order(n->left);

    // print n->value

    if (n->right)
        pre_order(n->right);
}

void in_order(struct Node* n) {
    if (n->left)
        pre_order(n->left);

    // print n->value

    if (n->right)
        pre_order(n->right);
}

Post-Order Traversal

void post_order(struct Node* n) {
    if (n->left)
        pre_order(n->left);

    if (n->right)
        pre_order(n->right);

    // print n->value
}

void post_order(struct Node* n) {
    if (n->left)
        pre_order(n->left);

    if (n->right)
        pre_order(n->right);

    // print n->value
}

Breadth First Traversal

Breadth first traversal traverses a tree by visiting all nodes at a given height, before descending the depth of the tree.

python

def bfs(self):
    queue = Queue()
    queue.put(self)

    while not queue.empty():
        current_node = queue.get()
        print(current_node.value)

        if current_node.left_child:
            queue.put(current_node.left_child)

        if current_node.right_child:
            queue.put(current_node.right_child)

def bfs(self):
    queue = Queue()
    queue.put(self)

    while not queue.empty():
        current_node = queue.get()
        print(current_node.value)

        if current_node.left_child:
            queue.put(current_node.left_child)

        if current_node.right_child:
            queue.put(current_node.right_child)

AVL Tree

Red-Black Tree

N-Ary Tree

Binary Search Tree

binarysearchtree

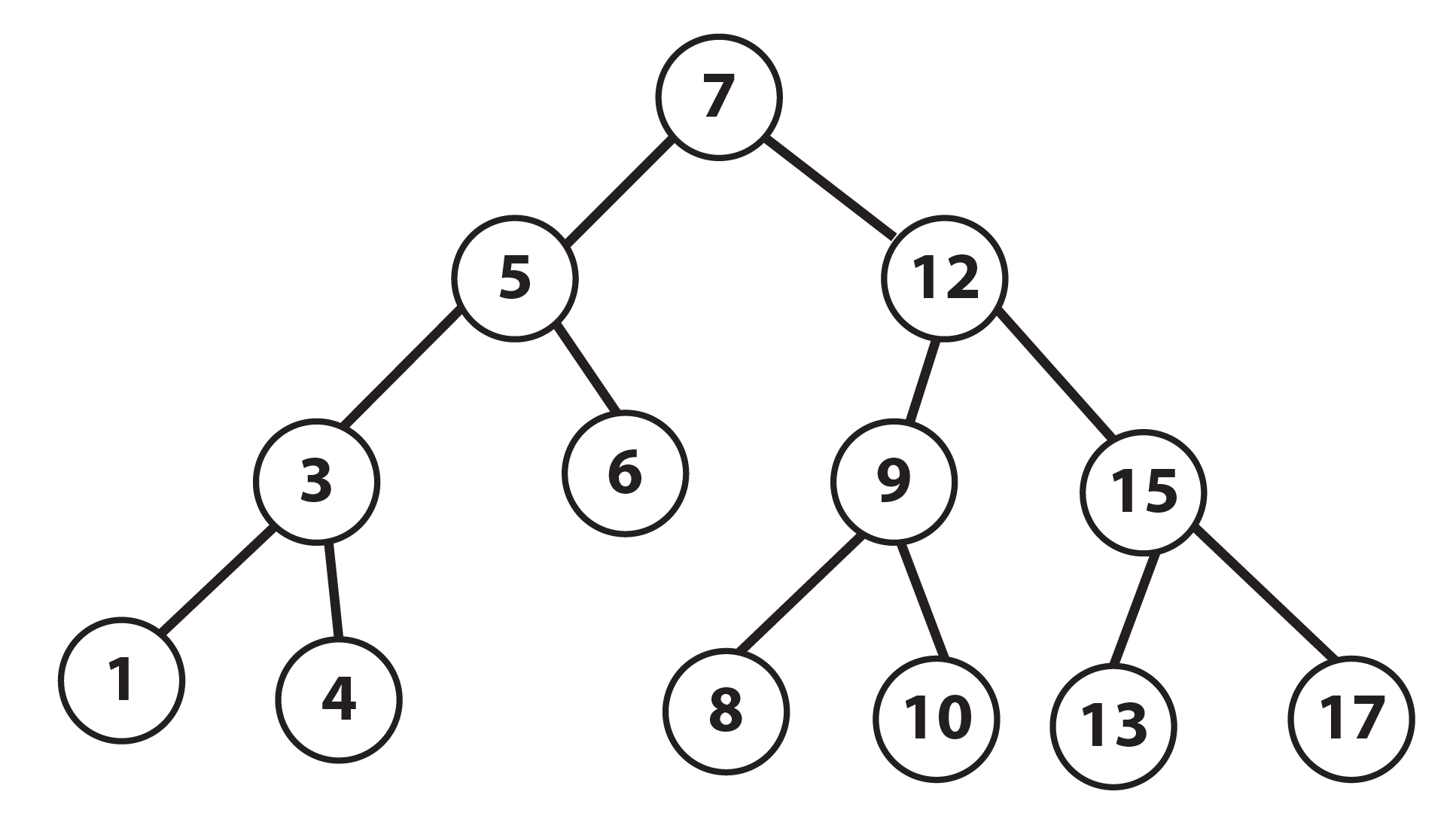
A Binary Search Tree is one in which the value of the node stored on the left is less than the value of root, and the value of the node on the right is greater than the value of the root. By organizing a tree in this way, values can easily be found using a similar method as binary search which eliminates half of the remaining possibilities at each step.

Searching

bool contains(Node* curr, int value) {
    if (curr->data == value) { return true; }
    else if (value < curr->value) {
        if (curr->left) {
            return contains(curr->left, value);
        }
    } else {
        if (curr->right) {
            return contains(curr->right, value);
        }
    }
}

bool contains(Node* curr, int value) {
    if (curr->data == value) { return true; }
    else if (value < curr->value) {
        if (curr->left) {
            return contains(curr->left, value);
        }
    } else {
        if (curr->right) {
            return contains(curr->right, value);
        }
    }
}

Inserting

To maintain the structure rules of the Binary Search Tree after insertion, the leaves of each node must be evaluated and the next route determined until a non-null spot that meets the criteria is determined. If the the current value of the node is greater than the value to be inserted, it will attempt to insert on the left if the left is currently null. If the left is not null, it will recursively evaluate the left node in the same way.

void insert(Node* new, Node* curr, int value) {
    if (value <= curr->value) {
        if (curr->left == NULL) {
            curr->left = new;
        } else {
            insert(curr->left, value);
        }
    } else {
        if (curr->right == NULL) {
            curr->right = new;
        } else {
            insert(curr->right, value);
        }
    }
}

void insert(Node* new, Node* curr, int value) {
    if (value <= curr->value) {
        if (curr->left == NULL) {
            curr->left = new;
        } else {
            insert(curr->left, value);
        }
    } else {
        if (curr->right == NULL) {
            curr->right = new;
        } else {
            insert(curr->right, value);
        }
    }
}

B-Tree

Stack

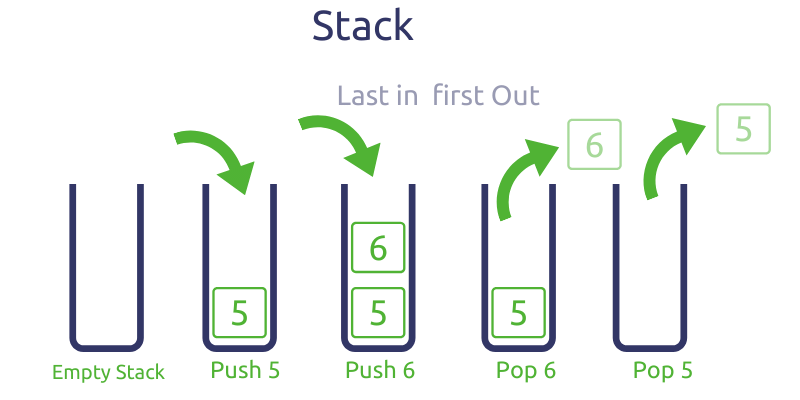
stack

Stack Array

A struct can be created which tracks the index of the top, and holds the allocated array. When popping a value, the array index should be wiped with null value and top decremented. If the top index is out of range, it should throw an error to indicate a stack underflow.

/*
* Stack implementation using array in C
*/

#define CAPACITY 100

typedef struct stack {
    int top;
    arr[CAPACITY];
} stack;

// Function to push a new element in stack
void push(stack* s, int val)
{
    s->arr[s->top++] = val;
}

// Function to pop element from top of stack
int pop(stack* s)
{    
    if (top < 0) return -1;
    return s->arr[s->top--];
}

/*
* Stack implementation using array in C
*/

#define CAPACITY 100

typedef struct stack {
    int top;
    arr[CAPACITY];
} stack;

// Function to push a new element in stack
void push(stack* s, int val)
{
    s->arr[s->top++] = val;
}

// Function to pop element from top of stack
int pop(stack* s)
{    
    if (top < 0) return -1;
    return s->arr[s->top--];
}

Dynamic Stack Using Linked List

When the size of the array is not known and allocating a static array of its capacity may be wasteful, Linked Lists can be used to connect the items on the stack. When popping an object, the node pointer should be stored in a temporary pointer, then free'd once the new top is the old node's next pointer.

/*
* Stack implementation using linked list in C
*/

// Define stack node structure
// The variable also instantiates this as a global
struct stack {
    int data;
    struct stack *next;
} *top;

// Function to push a new element in stack.
void push(int element)
{
    // Create a new node and push to stack
    struct stack* newNode = malloc(sizeof(struct stack));

    // Assign data to new node in stack
    newNode->data = element;

    // Next element after new node should be current top element
    newNode->next = top;        

    // Make sure new node is always at top
    top = newNode;
}

// Function to pop element from top of stack.
int pop()
{    
    // Check stack underflow
    if (!top)
    {
        printf("Stack is empty.\n");
        return -1;
    }
    // Hold pointer to node to be removed
    stack* old = top;
    
    int data = 0;
 
    // Copy data from stack's top element
    data = old->data;

    // Move top to its next element
    top = old->next;

    free(old);

    return data;
}

/*
* Stack implementation using linked list in C
*/

// Define stack node structure
// The variable also instantiates this as a global
struct stack {
    int data;
    struct stack *next;
} *top;

// Function to push a new element in stack.
void push(int element)
{
    // Create a new node and push to stack
    struct stack* newNode = malloc(sizeof(struct stack));

    // Assign data to new node in stack
    newNode->data = element;

    // Next element after new node should be current top element
    newNode->next = top;        

    // Make sure new node is always at top
    top = newNode;
}

// Function to pop element from top of stack.
int pop()
{    
    // Check stack underflow
    if (!top)
    {
        printf("Stack is empty.\n");
        return -1;
    }
    // Hold pointer to node to be removed
    stack* old = top;
    
    int data = 0;
 
    // Copy data from stack's top element
    data = old->data;

    // Move top to its next element
    top = old->next;

    free(old);

    return data;
}

Queue

A queue data structure is useful in many scenarios where you need to process elements in a first-in, first-out (FIFO) order.

Queues are particularly useful when:

You need to maintain order of arrival for processing.
You want to decouple different parts of a system for asynchronous processing.
You need to buffer or manage flow of data between different processes or systems.

By using queues in these scenarios, you can efficiently manage data flow, improve system responsiveness, and ensure fair processing of tasks or data in the order they arrive.

/*
*  Queue implementation using linked list in C
*/

// Define the structure for the queue
struct Queue {
    struct Node* front;
    struct Node* rear;
};

// Function to initialize an empty queue
struct Queue* queue_init() {
    struct Queue* queue = (struct Queue*)malloc(sizeof(struct Queue));
    queue->front = queue->rear = NULL;
    return queue;
}

// Function to check if the queue is empty
bool queue_is_empty(struct Queue* queue) {
    return (!queue->front);
}

// Function to enqueue (add an element to the rear of the queue)
void queue_enqueue(struct Queue* queue, int data) {
    struct Node* newNode = malloc(sizeof(struct Node));
    
    if (queue_is_empty(queue)) {
        queue->front = queue->rear = newNode;
    } else {
        queue->rear->next = newNode;
        queue->rear = newNode;
    }
}

// Function to dequeue (remove an element from the front of the queue)
int queue_dequeue(struct Queue* queue) {
    if (queue_is_empty(queue)) {
        return -1; // Or any other value to indicate an error
    }
    
    struct Node* temp = queue->front;
    int data = temp->data;
    
    queue->front = queue->front->next;
    
    // If front becomes NULL, set rear also as NULL
    if (!queue->front) {
        queue->rear = NULL;
    }
    
    free(temp);
    return data;
}

// Function to get the front element without removing it
int queue_front(struct Queue* queue) {
    if (queue_is_empty(queue)) {
        return -1; // Or any other value to indicate an error
    }
    return queue->front->data;
}

// Function to free the memory used by the queue
void queue_destroy(struct Queue* queue) {
    while (!queue_is_empty(queue)) {
        queue_dequeue(queue);
    }
    free(queue);
}

/*
*  Queue implementation using linked list in C
*/

// Define the structure for the queue
struct Queue {
    struct Node* front;
    struct Node* rear;
};

// Function to initialize an empty queue
struct Queue* queue_init() {
    struct Queue* queue = (struct Queue*)malloc(sizeof(struct Queue));
    queue->front = queue->rear = NULL;
    return queue;
}

// Function to check if the queue is empty
bool queue_is_empty(struct Queue* queue) {
    return (!queue->front);
}

// Function to enqueue (add an element to the rear of the queue)
void queue_enqueue(struct Queue* queue, int data) {
    struct Node* newNode = malloc(sizeof(struct Node));
    
    if (queue_is_empty(queue)) {
        queue->front = queue->rear = newNode;
    } else {
        queue->rear->next = newNode;
        queue->rear = newNode;
    }
}

// Function to dequeue (remove an element from the front of the queue)
int queue_dequeue(struct Queue* queue) {
    if (queue_is_empty(queue)) {
        return -1; // Or any other value to indicate an error
    }
    
    struct Node* temp = queue->front;
    int data = temp->data;
    
    queue->front = queue->front->next;
    
    // If front becomes NULL, set rear also as NULL
    if (!queue->front) {
        queue->rear = NULL;
    }
    
    free(temp);
    return data;
}

// Function to get the front element without removing it
int queue_front(struct Queue* queue) {
    if (queue_is_empty(queue)) {
        return -1; // Or any other value to indicate an error
    }
    return queue->front->data;
}

// Function to free the memory used by the queue
void queue_destroy(struct Queue* queue) {
    while (!queue_is_empty(queue)) {
        queue_dequeue(queue);
    }
    free(queue);
}

/*
*  Queue implementation using array in C
*/
#define MAX_SIZE 100

typedef struct {
    int items[MAX_SIZE];
    int front;
    int rear;
} Queue;

// Initialize the queue
void initialize(Queue *q) {
    q->front = -1;
    q->rear = -1;
}

// Check if the queue is empty
int isEmpty(Queue *q) {
    return (q->front == -1 && q->rear == -1);
}

// Check if the queue is full
int isFull(Queue *q) {
    return (q->rear + 1) % MAX_SIZE == q->front ? 1 : 0;
}

// Add an element to the queue
void enqueue(Queue *q, int value) {
    if (isFull(q)) {
        printf("Queue is full!\n");
    } else {
        if (isEmpty(q)) {
            q->front = 0;
        }
        q->rear = (q->rear + 1) % MAX_SIZE;
        q->items[q->rear] = value;
        printf("%d enqueued to queue\n", value);
    }
}

// Remove an element from the queue
int dequeue(Queue *q) {
    int item;
    if (isEmpty(q)) {
        printf("Queue is empty!\n");
        return -1;
    } else {
        item = q->items[q->front];
        if (q->front == q->rear) {
            // Last element in the queue
            initialize(q);
        } else {
            q->front = (q->front + 1) % MAX_SIZE;
        }
        printf("%d dequeued from queue\n", item);
        return item;
    }
}

// Display the queue
void display(Queue *q) {
    int i;
    if (isEmpty(q)) {
        printf("Queue is empty!\n");
    } else {
        printf("Queue elements: ");
        for (i = q->front; i != q->rear; i = (i + 1) % MAX_SIZE) {
            printf("%d ", q->items[i]);
        }
        printf("%d\n", q->items[i]);
    }
}

/*
*  Queue implementation using array in C
*/
#define MAX_SIZE 100

typedef struct {
    int items[MAX_SIZE];
    int front;
    int rear;
} Queue;

// Initialize the queue
void initialize(Queue *q) {
    q->front = -1;
    q->rear = -1;
}

// Check if the queue is empty
int isEmpty(Queue *q) {
    return (q->front == -1 && q->rear == -1);
}

// Check if the queue is full
int isFull(Queue *q) {
    return (q->rear + 1) % MAX_SIZE == q->front ? 1 : 0;
}

// Add an element to the queue
void enqueue(Queue *q, int value) {
    if (isFull(q)) {
        printf("Queue is full!\n");
    } else {
        if (isEmpty(q)) {
            q->front = 0;
        }
        q->rear = (q->rear + 1) % MAX_SIZE;
        q->items[q->rear] = value;
        printf("%d enqueued to queue\n", value);
    }
}

// Remove an element from the queue
int dequeue(Queue *q) {
    int item;
    if (isEmpty(q)) {
        printf("Queue is empty!\n");
        return -1;
    } else {
        item = q->items[q->front];
        if (q->front == q->rear) {
            // Last element in the queue
            initialize(q);
        } else {
            q->front = (q->front + 1) % MAX_SIZE;
        }
        printf("%d dequeued from queue\n", item);
        return item;
    }
}

// Display the queue
void display(Queue *q) {
    int i;
    if (isEmpty(q)) {
        printf("Queue is empty!\n");
    } else {
        printf("Queue elements: ");
        for (i = q->front; i != q->rear; i = (i + 1) % MAX_SIZE) {
            printf("%d ", q->items[i]);
        }
        printf("%d\n", q->items[i]);
    }
}

Heap

heap

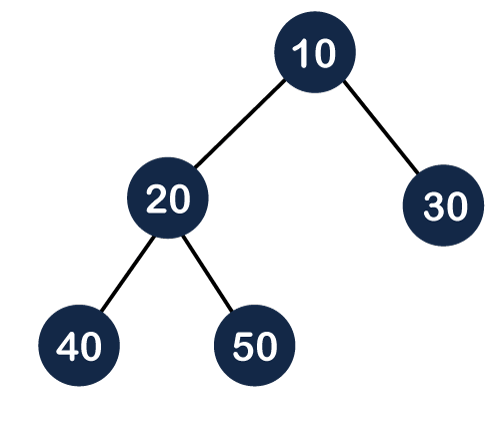
Maximum Heap

Minimum Heap

Hashes

hash

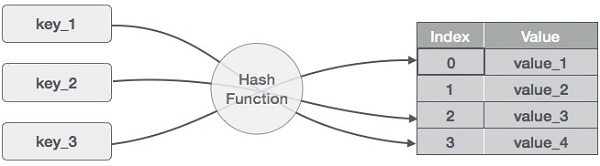
A hash map combines features of a static array and a linked list, without being bound by issues such as inserting new values in a size-defined array, or searching for values in a linked list. A hash map has a preallocated buffer, and uses the value of the data to be inserted to generate a key, or index by hashing it. If a hash is properly defined, there will be no hash collisions, and data with an indentical value will be stored in the identical spot in the hash map. This way, a value need only be calculated once, then stored in the hash map. Insted of generating the value again by calculation, the value can be retrieved from the hash map by visiting the pre-determined index.

The Hash Set is a hash map which stores no repeated values.

Code

int hash(int key) {
    int r = key % SIZE;
    return r < 0 ? r + SIZE : r;
}

void insert(int *values, int key, int value) {
    int index = hash(key);
    while (values[index]) {
        index++;
        index %= SIZE;
    }
    keys[index] = key;
    values[index]= value;
}

int search(int *keys, int *values, int key) {
    int index = hash(key);
    while (values[index]) {
        if (keys[index] == key) {
            return values[index];
        }
        index++;
        index %= SIZE;
    }
    return 0;
}

// The requested value is checked for, in each step of the loop 
// then the hash map is populated with the value if it doesn't 
// already exist. This means the check will take O(n)

int* main(int* nums, int numsSize, int target) {
    int keys[SIZE];
    int values[SIZE] = {0};
    for (int i = 0; i < numsSize; i++) {
        int complements = target - nums[i];
        int value = search(keys, values, complements);
        if (value) {
            int *indices = (int *) malloc(sizeof(int) * 2);
            indices[0] = value - 1;
            indices[1] = i;
            return indices;
        }
        insert(keys, values, nums[i], i + 1);
    }
    return NULL;
}

int hash(int key) {
    int r = key % SIZE;
    return r < 0 ? r + SIZE : r;
}

void insert(int *values, int key, int value) {
    int index = hash(key);
    while (values[index]) {
        index++;
        index %= SIZE;
    }
    keys[index] = key;
    values[index]= value;
}

int search(int *keys, int *values, int key) {
    int index = hash(key);
    while (values[index]) {
        if (keys[index] == key) {
            return values[index];
        }
        index++;
        index %= SIZE;
    }
    return 0;
}

// The requested value is checked for, in each step of the loop 
// then the hash map is populated with the value if it doesn't 
// already exist. This means the check will take O(n)

int* main(int* nums, int numsSize, int target) {
    int keys[SIZE];
    int values[SIZE] = {0};
    for (int i = 0; i < numsSize; i++) {
        int complements = target - nums[i];
        int value = search(keys, values, complements);
        if (value) {
            int *indices = (int *) malloc(sizeof(int) * 2);
            indices[0] = value - 1;
            indices[1] = i;
            return indices;
        }
        insert(keys, values, nums[i], i + 1);
    }
    return NULL;
}

Hash Functions

Simple Hash Function for Strings

int hash_function(char* key) {
    int hash = toupper(key[0]) - 'A'; 
    // Subtracting 'A' sets the index of alpha characters 
    // starting with 0 for 'A'. 'A' is 0, 'B' is 1, etc.
    return hash % SIZE; // Constrain to the array size
}

int hash_function(char* key) {
    int hash = toupper(key[0]) - 'A'; 
    // Subtracting 'A' sets the index of alpha characters 
    // starting with 0 for 'A'. 'A' is 0, 'B' is 1, etc.
    return hash % SIZE; // Constrain to the array size
}

If a collision occurs, linked lists can point to values with this same index.

A good hash value would distribute values evenly across the map.

Graph

graph

Bryan Melanson

Embedded Developer

Data Structures ​

Bitwise Operations ​

Operators ​

Common Operations ​

Set Bit ​

Clear Bit ​

Flip Bit ​

Clear ​

Little Endian to Big Endian ​

Big Endian to Little Endian ​

Array ​

Arrays in C ​

Static vs. Dynamic Arrays ​

Static Arrays ​

Dynamic Arrays ​

C Strings ​

Matrix ​

Normal Declaration ​

Dynamic Declaration ​

Linked List ​

Inserting ​

Deleting ​

Circular Linked List ​

Inserting ​

Deleting ​

Doubly Linked List ​

Inserting ​

Deleting ​

Binary Tree ​

Depth First Traversal ​

Pre-Order Traversal ​

In-Order Traversal ​

Post-Order Traversal ​

Breadth First Traversal ​

AVL Tree ​

Red-Black Tree ​

N-Ary Tree ​

Binary Search Tree ​

Searching ​

Inserting ​

B-Tree ​

Stack ​

Stack Array ​

Dynamic Stack Using Linked List ​

Queue ​

Heap ​

Maximum Heap ​

Minimum Heap ​

Hashes ​

Code ​

Hash Functions ​

Simple Hash Function for Strings ​

Graph ​

Bryan Melanson

Data Structures

Bitwise Operations

Operators

Common Operations

Set Bit

Clear Bit

Flip Bit

Clear

Little Endian to Big Endian

Big Endian to Little Endian

Array

Arrays in C

Static vs. Dynamic Arrays

Static Arrays

Dynamic Arrays

C Strings

Matrix

Normal Declaration

Dynamic Declaration

Linked List

Inserting

Deleting

Circular Linked List

Inserting

Deleting

Doubly Linked List

Inserting

Deleting

Binary Tree

Depth First Traversal

Pre-Order Traversal

In-Order Traversal

Post-Order Traversal

Breadth First Traversal

AVL Tree

Red-Black Tree

N-Ary Tree

Binary Search Tree

Searching

Inserting

B-Tree

Stack

Stack Array

Dynamic Stack Using Linked List

Queue

Heap

Maximum Heap

Minimum Heap

Hashes

Code

Hash Functions

Simple Hash Function for Strings

Graph